如图，把∠A的对边与∠A的邻边的比叫做∠A的正切，

记作 tan=∠A的对边/∠A的邻边=a/b

三角函数

例如: tan15°=2-√3

tan30°=√3/3

tan45°=1

tan60°=√3

正切函数是直角三角形中，对边与邻边的比值叫做正切。放在直角坐标系中

Tan 取某个角并返回直角三角形两个直角边的比值。此比值是直角三角形中该角的对边长度与邻边长度之比，也可写作tg。

正切tangent，因此在20世纪90年代以前正切函数是用tgθ来表示的，而20世纪90年代以后用tanθ来表示。

将角度乘以 π/180 即可转换为弧度，将弧度乘以 180/π 即可转换为角度。

在三角函数中:tanθ=sinθ/cosθ; tanθ=1/cotθ.

在Rt△ABC，∠C=90度，AB=c,BC=a,AC=b,tanA=BC/AC=a/b

将一个角放入直角坐标系中

使角的始边与X轴的非负半轴重合

在角的终边上找一点A(x，y)

过A做X轴的垂线

则r=(x^2+y^2)^(1/2)

tan =y/x

正切无最大最小值

tanA=∠A的对边/∠A的邻边

30° sina=1/2 cosa=√3/2 tana=√3/3

45° sinα=√2/2 cosα=√2/2 tanα=1

60° sinα=√3/2 cosα=1/2 tanα=√3

90° sinα=1 cosα=0 tanα不存在

120° sinα=√3/2 cosα=-1/2 tanα=-√3

150° sinα=1/2 cosα=-√3/2 tanα=-√3/3

180° sinα=0 cosα=-1 tanα=0

270° sinα=-1 cosα=0 tanα不存在

360° sinα=0 cosα=1 tanα=0

1、定义域:{x|x≠(π/2)+kπ,k∈Z}

2、值域:实数集R

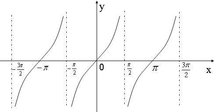3、奇偶性:奇函数

4、单调性:在区间(-π/2+kπ,π/2+kπ)，(k∈Z)上是增函数

5、周期性:最小正周期π(可用T=π/|ω|来求)

6、最值:无最大值与最小值

7、零点:kπ,k∈Z

8、对称性:无

轴对称:无对称轴

中心对称:关于点(kπ/2,0)对称 (k∈Z)

9、奇偶性:由tan(-x)=-tan(x)，知正切函数是奇函数，它的图象关于原点呈中心对称

10、图像(如图所示)

实际上，正切曲线除了原点是它的对称中心以外,所有x=(n/2)π (n∈Z) 都是它的对称中心.