1、对于两个向量a（向量a≠向量0），向量b，当有一个实数λ，使向量b=λ向量a（记住向量是有方向的）则向量a‖向量b。反之，当向量a‖向量b时，有且只有一个实数λ，能使向量b=λ向量a。
2、当向量a=(x1,y1)，向量b=(x2,y2)时，当x1y2=x2y1时，向量a‖向量b，反之也成立。

平行向量用法：

1、加法运算

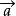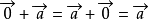对于零向量和任意向量  ，有：  。向量的加法满足所有的加法运算定律。

三角形法则：已知从点A出发的向量 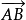 与从点B出发的向量 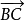相加，则以A为起点的向量  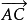即为它们之和。

平行四边形法则：已知两个从同一点O出发的两个向量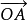 、 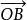，以OA、OB为邻边作平行四边形OACB，则以O为起点的对角线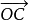向量  就是向量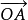 、  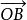的和，这种计算法则叫做向量加法的平行四边形法则。

2、减法运算

与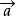 长度相等，方向相反的向量，叫做  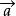的相反向量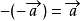，  ，零向量的相反向量仍然是零向量。（1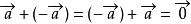）  ；（2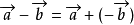）  。以减向量的终点为起点，被减向量的终点为终点(三角形法则)。